首先回顾一下克莱姆法则,再看如何在没有矩阵概念、矩阵运算的情况下快速证明它。注意,本文只考虑实数域。
1克莱姆法则
克莱姆法则 如果行列式 不为 ,则线性方程组 的唯一解 由下式给出,
其中 是指将 的第 列替换为 得到的矩阵。尽管克莱姆提出法则后过了一百年才有矩阵的概念,但这里为了方便描述,还是使用了矩阵。

〄 瑞士数学家克莱姆(1704~1752)
瑞士数学家克莱姆()于 1750 年在他的一本著作的附录中发布了该法则。为了确定经过 5 个点的一般二次曲线的系数,他应用了这个法则,即由线性方程组的系数来计算解。
不过,这个法则经常出现在历史命名错误列表中(即那些众所周知的、但实际上并不是以始发者命名的数学定理或概念)。
有学者声称,苏格兰数学家麦克劳林()早在 1729 年就发现克莱姆法则,并将其写入他于 1748 年出版的《论代数》中。
实际上,克莱姆和麦克劳林都写下了一个由 3 个线性方程和 3 个未知数组成的线性方程组的解,其形式为两个量之比,每个量都是 6 个乘积之和。
但他们都没有给出任何证明,而只是推测了一般情况对应的公式。而且,麦克劳林给出的为每个乘积选择合适符号的规则是错误的。相反,克莱姆的想法是由给定排列的置换次数来确定符号。这么看来克莱姆,这个法则冠名克莱姆还是说得过去的。
行列式的定义
给定一个 矩阵 , 的行列式定义为一个标量,
其中,总和取决于 的 个置换 。
插播一段,这里其实有另外一个数学概念,那就是群。上面这个置换对应的就是对称群 。
我们以 时的对称群 举例说明。下图中上面 个表示旋转对称,分别对应顺时针(当然也可以取逆时针)旋转 度、 度和 度,下面 个表示翻转、翻转+旋转 度和翻转+旋转 度。用这 6 个刻画三角形的对称就足够了,可以对照看看是否能构成一个群。
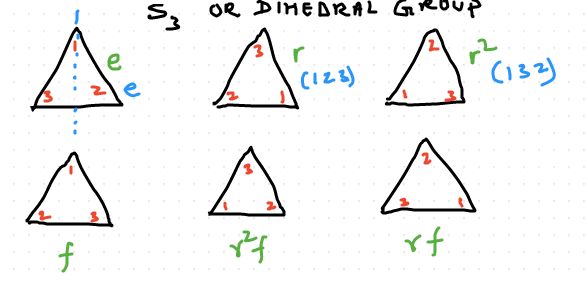
回到定义,乘积 有 个数,第 个数是从第 行中选第 列中的那个元素,而且每个乘积都是从 的每一行和每一列中仅选取一个元素。 的行列式可以用 或 表示。需要注意的是,这里的矩阵 是方阵,并没有为非方阵定义行列式。
看了上次,现在再看到上面这个定义应该不会惊讶了吧。
另外,行列式相关的另一个概念(拉普拉斯展)将发挥重要作用。对于矩阵 ,我们先定义它的元素 的代数余子式 ,即
其中 是元素 的余子式,即从 中删除第 行和第 列所得的 矩阵的行列式。
行列式 其实是一个关于矩阵元素的函数,可以求关于元素 的偏导,结果就是上面的代数余子式 。由这个概念还可以得到如下定理。
拉普拉斯定理 令 和 为集合 中的整数,则有
这个定理的上面部分可以由行列式的定义直接推得,下面部分相当于有两列或两行相同,各位不妨自己证一下。

〄 法国数学家拉普拉斯(1749~1827)
补充一点,当有了矩阵的概念,还可以由上式直接得到逆矩阵。从上面定理很容易可以得出,非奇异矩阵 的逆 具有如下形式,
其中 称为 的伴随矩阵,它是辅助矩阵 的转置,而 的第 个元素为 。
2克莱姆法则的证明
虽然 1750 年就提出了克莱姆法则,但一直没有证明,第一次证明大概在 1825 年左右,但那个证明晦涩冗长,也没有太多价值。
所以这里推荐看一下德国著名数学家雅可比()基于拉普拉斯定理给出的一个十分简洁的证明。雅可比这个名字很熟悉吧,后面还会经常出现。

〄 德国数学家卡尔·雅可比(1804~1851)证法1
证明: 固定 中的一个整数 ,将第 个方程乘以 ,得
然后将 个方程加起来,得
根据拉普拉斯定理,上式左侧唯一的非零项是第 项,并且 前的系数刚好等于 。看右侧,刚好是将 的第 列用 代换后的行列式,即 。因此得,
证毕
证法 2
另外,上面是在没有矩阵的概念时给出的证明。等引入矩阵的概念后,会引出更多的证明。例如,因为 不是奇异的,所以线性方程组 两边左乘逆矩阵 ,得 ,将上文中求逆矩阵的公式代入,得
上面最后那项的分子是一个向量,由拉普拉斯定理/展开可知,向量的第 个元素刚好是 。因此,解 的第 个分量 为,
证毕
好了,关于行列式以及克莱姆法则的来龙去脉以及证明就讲到这里。为了保持短小精悍克莱姆,行列式的一些性质以及应用就放到后文吧。
最后,封面图片你看懂了吗?

限时特惠:本站每日更新海量各大内部副业创业课程,一年只需98元,全站资源免费下载!点击查看会员权益
站长微信:CGXDP666